pythonを使って積分計算をする機会があった。 備忘にここにまとめておく。
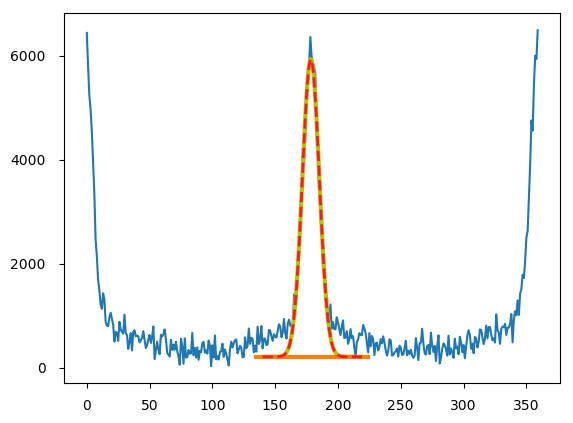
データは上の図の青ラインのようなガビガビの散布データ。 numpyの360行のarrayに入っている。 横軸は360度の角度で縦軸は強度。 やりたかったことは1度刻みで強度を持つデータに、その角度ごとに三角関数をかけてからその総和を取るということ。
過去の文献をのぞいて見るとシグマで計算している人とインテグラルで計算している人がいる。 もともとの式の定義はインテグラル。 なのでインテグラルを選択するのが順当だろうけど、せっかくなのでpythonを使ってできる計算を色々と書いてみようと思い立った。
まずできるのはデータポイントごとに、三角関数の計算をしてそれからnumpy.sumをとってのシグマ計算。 それからやっぱり積分計算の方が良いかと思い、同じプロセスからnumpy.trapzを使っての積分計算。 とはいってもポイントごとの値のばらつきが大きいデータなのでやっぱりピークフィットしてから、その関数を使って積分計算をかけた方が良いかなとも思い、scipy.integral.quadを使っての積分計算。
というわけでこれらの方法での結果と実行速度を比べてみることにした。
生データでのシグマ計算
まずは横軸を0度から359度まで作っておく。 ついでに三角関数用にradianも準備しておく。 例のごとくimportは省略。 numpyとscipy、lmfit、それからTimeくらいかな今回は。
pix = np.linspace(0,359,360) AzTheta = np.radians(pix)
コンスタントバックグラウンドの準備。 ガビガビのデータなので外れ値を引いてもしょうがない。 numpy.nanminを使って適当な範囲で適当な最小値を選択。
const = np.ones(90)*np.nanmin(Int[140:220])
バックグラウンドを引いたピークの裾からピークトップまでのデータ。 それから各データポイントにそれぞれ0から90度までのsinとcosをかけた式。
eqsum = (Inttheta[88:179]-const) eqsin = (Inttheta[88:179]-const)*(np.sin(AzTheta[0:91])) eqsin = (Inttheta[88:179]-const)*(np.cos(AzTheta[0:91]))
そうしたらsumを使ってarrayの総和をとる。
sum1 = np.sum(eqsum) sum2 = np.sum(eqsin) sum3 = np.sum(eqcos)
printで出力。
sum1 66885.0328331 sum2 61156.5549622 sum3 15573.1626916 Calculation time: 0.0002231597900390625[s]
生データからのインテグラル計算
上と同じものをsumではなくnumpy.trapzで計算。 trapzはtrapezoidal ruleでの積分計算。 関数じゃなくても生データから積分計算ができる。
sum1 = np.trapz(eqsum) sum2 = np.trapz(eqsin) sum3 = np.trapz(eqcos)
1度刻みのデータなので少しだけ総和よりも小さくなるのは想定通り。 しかしtrapzの方が速度が早かったのは少し意外。
sum1 63719.308712 sum2 58081.6139909 sum3 15482.3795419 Calculation time: 0.00015211105346679688[s]
フィッティングからのインテグラル計算
こちらはscipyのintegrate.quadを用いて。 フィッティングは以前書いたので省略。 私はいろいろ便利なのでlmfitを使っている。 投稿下にカーブフィッティングへの関連記事リンクを貼っておいた。 ここではconstantバックグラウンドとareaGaussianでフィットした(上の図の赤点線)。
それから積分用の関数を書く。 シンプルなX依存の関数ならそのままintegrate.quadの中に式を書けば良い。
他のパラメータが入る式を使いたい時は先に式を定義しておく。 それからintegrate.quadのargsでパラメータの値を指定することができる。 今回のように最初に関数のフィットをして、その結果の値を積分に突っ込みたいときにはこの方法が便利だと思う。
def eq1(x, amp, cen, hf): return amp*(2/hf)*np.sqrt((np.log(2)/np.pi))*np.exp((-4*np.log(2))*((cen-x)/hf)**2) def eq2(x, amp, cen, hf): return (amp*(2/hf)*np.sqrt((np.log(2)/np.pi))*np.exp((-4*np.log(2))*((cen-x)/hf)**2))*(np.sin(np.radians(x))) def eq3(x, amp, cen, hf): return (amp*(2/hf)*np.sqrt((np.log(2)/np.pi))*np.exp((-4*np.log(2))*((cen-x)/hf)**2))*(np.cos(np.radians(x)))
式のパラメータにカーブフィッティングのベストの値をresult.best_values.getを使って代入。 それから0から90まで積分計算を行う。
s1 = sp.integrate.quad(eq1, 0, 90, args = (result.best_values.get('g1_amp'),90,result.best_values.get('g1_hf')))
s2 = sp.integrate.quad(eq2, 0, 90, args = (result.best_values.get('g1_amp'),90,result.best_values.get('g1_hf')))
s3 = sp.integrate.quad(eq3, 0, 90, args = (result.best_values.get('g1_amp'),90,result.best_values.get('g1_hf')))
生データはピークの裾が持ち上がっているので、フィットしてからの積分値はだいぶ値が異なっている。 それをどう解釈するかはデータ次第。
フィットをもうちょっと真面目にするとしたらVoigtなどを使ってフィットしても良いし。 このデータの場合だと生データのバックグラウンドの取り方を変えても値は近くなるかな。
sum1 48043.715584253885 sum2 47717.13305405471 sum3 4456.932291343271
時間はフィッティングも合わせるとだいぶ遅い。 積分だけでも生データより10倍遅くなっている。 とはいえよっぽど大量のデータ処理じゃなければ問題はない速度。
total time: 0.011394023895263672[s] integration time: 0.002457857131958008[s]
というわけで結構値が変わるので、どう計算するかを結構慎重に考える必要がある。 大体の場合先行研究をいくつか見れば答えが書いてあるのだけれど。
関連記事
D